III. Origin and Propagation of Cosmic Rays

Main research topics:

• Cosmic ray and MHD wave driven galactic winds

• Transport of cosmic ray nucleons and modeling of diffuse gamma-ray emission

• Transport of cosmic ray electrons and modeling of radio continuum emission

• Acceleration of cosmic rays in galactic outflows

Cosmic Rays (CRs) are the high energy component of the ISM and consist of nucleons and electrons (and high energy photons). The nucleonic component is dominating the energy and number content and has roughly interstellar abundances (with some important exceptions). This already suggests that so-called CR primaries (as opposed to secondaries, which are generated by nucelar reactions with primaries and the ISM gas through which they propagate) are accelerated ISM gas charged particles. The most striking observation of primary CRs is their power law differential energy flux spectrum dN(E) ~ E^-(q+1) dE (where q is the power law spectral index) between 10⁹ and 10¹⁴ eV and again between 3 10¹⁵ and 10¹⁹ eV (s. Fig. 1), with the highest energy particles reaching up to 10²¹ eV. This corresponds to an energy of up to 50 J, reminiscent to the kinetic energy of a tennis ball, thereby dwarfing energies attainable in terrestrial accelerators by more than a billion times. This poses a tremendous challenge for any explanation of their sources of acceleration. As CR particles are charged and therefore strongly interact with the ubiquitous magnetic field in the ISM, their arrival direction measured by earth and space borne detectors does not give any information on the location of their sources (the anisotropy in distribution is minute, about 10^-4 for the galactic CRs, and well understood in terms of their streaming). Due to the steepness of the energy flux spectrum the number of particles is significantly decreasing with energy, and therefore the highest energy particles require huge terrestrial detectors. For example particles with energies above 10¹⁹ eV hit the earth at a rate of 1 per square kilometer per year.

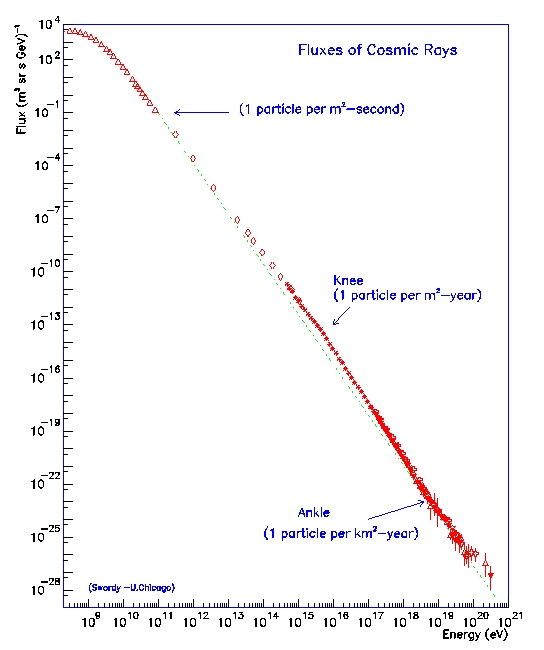Fig. 1: CR particle flux as a function of energy (data are accumulated from different experiments). The spectrum exhibits two breaks, on at 3 10¹⁵ eV ("knee") and a second one at 10¹⁹ eV ("ankle"). Below 1 GeV the particle flux is affected by modulation of the solar wind (figure credits to J. Cronin, T.K. Gaisser, and S.P. Swordy, Sci. Amer. 276, 44 (1997). 

A natural explanation of a power law spectrum is given by a process in which particles are stochastically accelerated and possess an energy dependent escape probablility from the site of acceleration. There exists now strong evidence that supernova remnant shock waves represent such a cosmic accelerator. According to the most popular theory, the so-called first order Fermi mechanism, particles cross a shock many times, gaining momentum during each crossing of the order v/c (particle velocity over speed of light, hence first order). It is hypothesized that magnetic field irregularities (e.g. MHD waves) frozen into the plasma reflect particles back and forth across the shock before they are convected eventually away downstream of the shock. Since the particles are deflected many times by these irregularities before a shock crossing, they perform a random walk, which can be physically described by diffusion. Therefore the whole process is also called diffusive shock acceleration  (DSA). The finite extension and hence maximum age of a supernova remnant shock implies a limitation in the maximum attainable CR proton energy to about 10¹⁴ - 10¹⁵ eV. Particles with energies above this and up to a few times 10¹⁶ eV are often explained as the result of rigidity (particle energy per unit charge, i.e. R = p c/(e Z), where Z is the nuclear charge, p the particle momentum, and e the elementary charge) dependent subsequent cut-offs of heavier elements from protons up to Fe. At still higher energies, i.e. above 10¹⁸ eV, the gyroradius of an accelerated particles is comparable to or larger than the size of a Galactic accelerator and therefore DSA would naturally cease to work. It is therefore assumed that higher energy particles are of extragalactic origin.

Our group is active in testing models, in which Galactic CRs are reaccelerated in galactic wind shocks, and thus should be able to explain the particle spectrum between the "knee" (at around 3 10¹⁵ eV) and the "ankle" (10¹⁹ eV) .

One may ask what happens to CRs over the life time of a galaxy. Does their number steadily increase or is it constant as a result of the balance between their generation and subsequent energy losses due to spallation processes with interstellar nuclei until they become nonrelativistic? The answer is somewhat more intricate. First of all it is clear that due to their enormous energies, CRs are not bound to a galaxy. However, they do not escape right away at the speed of light, because of their strong interaction with the interstellar magnetic field. In particular they can be deflected strongly by magnetic field perturbations (e.g. Alfven waves) and thus perform a random walk in the ISM, which can be described by a diffusion process (with an unfortunately poorly known diffusion coefficient). In essence, the CR transport velocity is reduced from the speed of light to about the Alfven speed (typically more than a 1000 times less). So wherever they are accelerated, they should be able to reach the edge of a galaxy in some 10⁷ years. But there is more information from so-called cosmic ray clocks. These are secondary CR particles resulting from nuclear interactions with ISM gas during CR propagation and involve radioactive isotopes such as ¹⁰Be, with a half life time of 1.5 million years, which is neither generated through the big bang nor through stellar nucleosynthesis to any significant amount. Hence the amount of ¹⁰Be (amongst other isotopes) measured near earth gives a direct hint of their residence time in the galaxy, which is of the order of 20 million years. This is surprisingly at odds with the time scale calculated from the CR secondary to primary ratio. From this one can infer (via some laborious nuclear transfer equation calculations) the amount of the energy dependent gas column density traversed by CR particles, the so-called grammage, which is about 10 g cm^-2 for a 1 GeV proton. For an average ISM gas density of 1 per cm³, this would imply a propagation time scale of the galactic disk of only a few million years. The discrepancy must arise because of the average density a particle sees being lower by a factor of 3 - 4, and hence the particle must diffuse most of the time in a lower density region, i.e. the galactic halo. Therefore their confinement volume is at least 3 times larger than the gas disk. In summary, CRs diffuse through the ISM and the galactic halo, and escape in an energy dependent fashion from the galaxy in about 20 million years for the typical 1 GeV particle. Therefore galactic CRs have to be constantly replenished, consistent with the idea that they are accelerated in processes linked to star formation.

However, it is often ignored that CRs, as they stream away from the galaxy, can couple efficiently to the gas via the MHD waves they are scattered off as a mediator. This leads to a significant momentum transfer from the CRs to the gas and hence to the formation (or support) of a galactic wind.

Cosmic ray driven galactic winds

The interaction between CRs and MHD waves is very complicated in detail and not fully understood yet. The description of CR acceleration and transport is usually described in the framework of the change of their distribution function in phase space (spanned by particle momentum and location) and can be derived from Liouville's theorem, leading e.g. to a so-called Fokker-Planck type equation for the particles. Considering the wave particle interaction, the distribution function can be expanded with the zero order term being its isotropic part. As long as the CRs are scattered efficiently by the waves their distribution function is largely isotropic. However, as particles stream away from the galaxy, a spatial gradient is induced and the number of scatterings in the forward and backward directions differs, leading to the growth of the higher order terms and to a non-isotropic distribution of the particles as seen in the frame of the MHD waves. This in turn calls for a so-called streaming instability, which tries to remove its cause. What happens physically is that waves, owing to a gyro-resonance condition (i.e. particles with gyroradii of the order of the wavelength of the waves), can grow exponentially and thus increase the scattering of the particles to such an extent that their distribution function becomes momentarily isotropized in the wave frame. This however leads to a transfer of momentum in the forward direction and hence to an acceleration of the gas away from the galaxy.

We have included these processes into the hydrodynamical equations by deriving appropriate cosmic ray hydrodynamical equations (essentially using the corresponding moments of the distribution function), which have been solved together numerically in a flux tube geometry (s. Fig. 2) 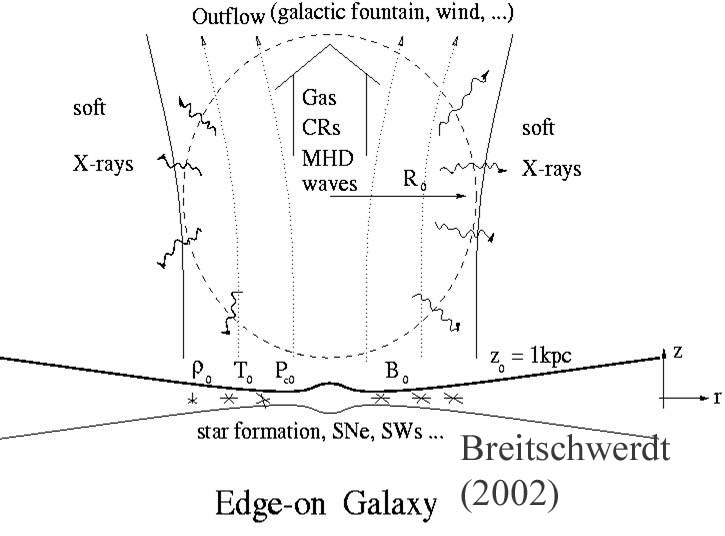for a steady-state model of the galactic outflow, thus describing a CR driven galactic wind 

Fig. 2: Schematic edge-on view of a star forming galaxy with a vertical magnetic field component. At a distance of about 1 kpc from the disk a CR and wave driven galactic wind forms, the dynamical siganture of which can be observed in soft X-rays (see NEI modeling above).

(Breitschwerdt et al. 1991, Astron. Astrophys. 245, 79; Breitschwerdt et al. 1993, Astron. Astrophys. 269, 54). In our model CRs are allowed to resonantly generate Alfvén waves, which couple the particles to the gas and result in a CR and wave pressure contribution tothe momentum equation. Together with a wave energy exchange equation this leads to a self-consistent description of an outflow, which will persist as long as the CR coupling is sufficiently strong. Even wave damping (ion-neutral damping or nonlinear Landau damping) cannot suppress a wind as the wave amplitude level does not need to be very large. We have estimated that a quiescent CR driven wind can exist during most time of the galactic evolution of our Milky Way, with a mass loss rate of the order of 0.3 solar masses per year. A later version of the model (Zirakashvili et al. 1996, Astron. Astrophys. 311, 113) includes galactic rotation, and hence allows for centrifugal force support of the wind. As a result, the galaxy may lose angular momentum, albeit not at a large rate.