Theory of the Interstellar Medium (ISM)
Main research topics
- Dynamical evolution of ISM on large and small scales
- Study of interstellar turbulence and its effect on ISM structure
- Investigation of interaction of ISM components
- Local Bubble and neighbouring superbubbles
- Comparison of models with observations (from radio to X-rays)
The ISM consists of various components which control the evolution of galaxies: Interstellar Gas, Magnetic Fields, Cosmic Rays, Photon Field, Dust.
Interstellar Gas
The classical concept of the state of the interstellar gas is the so-called 3-Phase-Model, which asserts that the gas is distributed over 3 stable phases in pressure equilibrium, the cold neutral medium (CNM), the warm neutral and ionized medium (WNM and WIM, respectively), and the hot intercloud medium (HIM), supplemented by the molecular medium (MM), which, however, is gravitationally bound and hence not in pressure equilibrium. The definition of a phase implies the stability of a gas element with respect to constant pressure perturbations. Owing to the interstellar net heat loss curve (giving the difference between total heating and cooling rate), which has a point of inflexion, there exist two stable points, defining the CNM and WNM, whereas the state of the DIG is maintained by interstellar UV radiation fields, and the HIM marks the upper end of the cooling curve. Recently this standard picture has been challenged, and our group has been actively involved in this work. It now appears that a large mass fraction, e.g. 50% of the warm gas between 500 and 5000 K, is in the thermally unstable regime. In addition, while the MM is distributed into clouds, often having a fractal structure, the CNM is rather filamentary, the WNM and DIG are extended sheets, and the HIM is tenuous with a volume filling factor near the solar circle of roughly 20%, instead of 50% or higher as was believed previously.
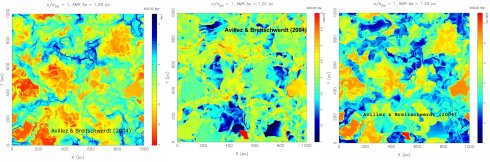

- © Avillez & Breitschwerdt
- Fig 1.: ISM pressure, temperature and density (from left to right) from 3D high resolution simulations on parallel machines for sections through an area of the Milky Way disk after 400 million years of evolution. The structure of the ISM is driven by supernova explosions, occurring at the observed rate (for details see Avillez & Breitschwerdt 2004), which generate a substantial amount of turbulence due to shear flows. The x- and y-axis range stretch out to 1000 pc and the colour coding is (from bottom to top of the bar): $10^{-1} < P/K < 10^5 {\rm K\,cm^{- 3}} $ (left), $10^1 < T < 10^{7.5} {\rm K}$ (middle), $10^{- 4} < n < 10^{2.5} {\rm cm^{- 3}}$ (right).
The key to this change in paradigm lies in the nature of compressibility of the ISM gas and its high Reynolds number (105-107). The flow is driven by supernova explosions from massive stars with more than 8 solar masses. Thus the flow, as by the way most flows in nature, is highly turbulent. Consider walking down a street surrounded by high buildings, and you will experience winds gusting down on the sidewalk. The reason is that a turbulent boundary layer is generated by the air flow, which in turn leads to the generation of vorticity (rotation of velocity field, curl(u)) and hence to turbulent eddies oozing out of the boundary layer.
The reason that flows can become turbulent lies in the non-linear nature of the Navier-Stokes equation, $$\frac{{\rm D}u}{{\rm D}t} =-\nabla \frac P\varrho + ν \nabla^2 u \;,$$ notably in the term $(u\nabla)u$ (where $ν$ is the kinematic viscosity of the flow). Taking the curl of this equation and using the vector identity $$\nabla\frac{u^2}2=(u\nabla)u+u \times \omega\;,$$ we obtain the vorticity equation $$\frac{{\rm D}\omega}{{\rm D}t} = (\omega\nabla)u + ν\nabla^2\omega\;,$$ where ${\rm D/D}t$ is the usual convective derivative. The interpretation of this equation is straightforward. But first consider the angular momentum of a spherical blob: $H = 1/2 I\omega$, where $I$ is the moment of inertia. Conservation of angular momentum yields ${\rm D}H/{\rm D}t = \tau_v$, where $\tau_v$ is the viscous torque acting on the blob. The left hand side consists of the terms $$I \frac{{\rm D}\omega}{{\rm D}t} + \omega \frac{{\rm D}I}{{\rm D}t}\;,$$ and thus we obtain $$I \frac{{\rm D}\omega}{{\rm D}t} = -\omega \frac{{\rm D}I}{{\rm D}t} + 2 \tau_v\;.$$ An increase in vorticity can therefore be due to the stretching of the blob, e.g. deforming it from a spherical into a cigarlike shape, thus decreasing its moment of inertia.This is called vortex stretching. A familiar example may be a tornado, in which the rising air is channeled into a hoselike configuration of converging streamlines, by which vorticity may be considerably increased. Returning to the vorticity equation, we now know that the first term on the rhs corresponds to vortex stretching. This can also be seen if we look at the velocity component parallel to the vortex tube, $u_\parallel$. Thus $(\omega\nabla)u_\parallel = |\omega| {\rm d}u_\parallel/{\rm d}s$, where ${\rm d}s$ is the line element along the vortex tube. Now stretching corresponds to $u_\parallel$ increasing along $s$, which means ${\rm d}u_\parallel/{\rm d}s > 0$, which is equivalent to an increase in $\omega$. The second term on the lhs describes the transport of vorticity by diffusion. Just like heat, vorticity can neither be created nor destroyed within the interior of a flow, but vorticity can be advected and spread by diffusion. This means that turbulence will cover a progressingly larger and larger region. This should be kept in mind, when we now turn to the evolution of supernova driven turbulence in the ISM.
We have performed high resolution numerical simulations (Avillez & Breitschwerdt 2004, Astron. Astrophys. 425, 899; 2005, Astron. Astrophys. 436, 585) of the ISM (with and without magnetic field) over an area of 1kpc x 1 kpc in the Galactic disk, centred on the solar circle, and extending 10 kpc perpendicular to it on either side of the disk, in order to capture the flow out of the disk, driven by supernova explosions. It is found that this so-called galactic fountain is essential for regulating the disk pressure, and hence curtailing the volume factor to lower values than previously assumed. The results show (see figures) that the ISM is far from pressure equilibrium, in contrast to what simple models predict. Even away from SN explosions, there are pressure variations of more than an order of magnitude. We observed that between 102-106 K, the ISM is ram pressure dominated, with shear flows generating a substantial amount of turbulence. And it is again the turbulence which can suppress the cooling instability as the gas does not have enough time to cool due to turbulent transport. It should be emphasized that in our simulations, turbulence is generated self-consistently by supernova induced shear flows, in contrast to other work, in which turbulence is driven by artificial forcing.
Magnetic Fields
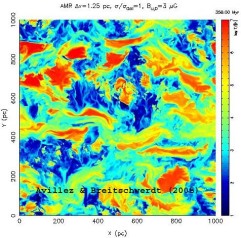

- © Avillez & Breitschwerdt
- Fig 2: ISM temperature distribution in a 1000 pc x 1000 pc region of the Milky Way centred on the solar circle after 400 million years of supernova explosion activity simulated on parallel processors. The colour coding ranges from 10 K (blue) to 107 K (red).
Large scale numerical 3D simulations with adaptive mesh refinement have also been performed in the ISM with an initially disk parallel magnetic field. Subsequently, stellar winds and supernova explosions have been followed, and the disruption of the upper disk and the evolution of superbubbles has been followed closely at high resolution (Avillez & Breitschwerdt 2005).
The most noticeable result is that supernova break-out of the disk does still occur even in the presence of an obstructing, initially plane parallel to the disk magnetic field, although the bubbles become now progressively elongated (in direction of the field) due to magnetic tension forces (see red regions in Fig. 2). Therefore the volume filling factors of the cold, warm and hot gas are not much different from the pure hydrodynamical case.
Cosmic Rays
See Cosmic Rays.
Local Bubble
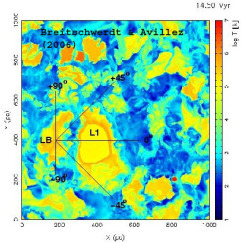

- © Breitschwerdt & Avillez
- Fig. 3a: The present day temperature distribution and extension of the Local Bubble (labeled LB) and the Loop I superbubble (L1) in a section through the galactic midplane. The solar system is located at the intersection of two lines of sight in the LB drawn in the plot.
The Local Bubble (LB) is a region of roughly 200pc diameter in the Milky Way disk, and stretching about 600 pc perpendicular to it. It is deficient of HI and copiously emitting in EUV and X-rays. It harbours small clouds, one of them being the so-called Local Cloud (LIC), into which our solar system is embedded. Most likely, the LB is a local superbubble created by successive supernova explosions in the past. However, there is no direct evidence of a local OB star association, which could have hosted supernova progenitors. On the search for its origin, we have therefore analyzed data of position, proper motions and radial velocities of stars using the Hipparcos astrometry satellite data base, and found that a moving group - the subgroup B1 from the Pleiades - was passing through the region now occupied by the LB (Berghöfer & Breitschwerdt 2002, Astron. Astrophys. 390, 299). During its passage, about 20 supernovae must have exploded, according to the subgroup's missing stars, derived from a so-called initial mass function (IMF) distribution for massive stars. A more recent analysis by us (Fuchs et al. 2006, Mon. Not. Roy. Astron. Soc. 373, 993) in a total region of 400 pc diameter centred on the solar system has basically confirmed these results, and has allowed us to determine the age of the LB starting with its first explosion to have occurred about 14.5 million years ago.
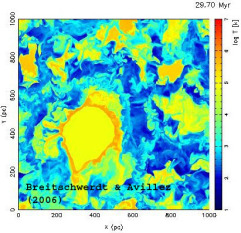

- © Breitschwerdt & Avillez
- Fig. 3b: Same as Fig. 3a, but about 14 million years from now, predicting that the LB will have been merged into the Loop I superbubble. Note also that the LB temperature will be considerably lower. The colour coding in both figures ranges from 10 K (blue) to 107 K (red).
In subsequent numerical high resolution 3D simulations, we (Breitschwerdt & Avillez 2006, Astron. Astrophys. Letters 452, L1) have put the LB and the neighbouring superbubble Loop I for the first time into a pre-evolved ISM (representing 200 million years of ISM evolution). In addition, we used the time and exact locations of the supernova explosions from our Hipparcos analysis, thus deriving the present day LB structure, in agreement with observations, and predicting its future merging with the Loop I bubble in about 14 million years (see Fig. 3). Moreover, our studies can explain the low amount of the ion O5+ found from UV measurements with the FUSE satellite, which was previously found difficult to reproduce by conductive interfaces. Our results show a more realistic distribution of turbulent mixing layers, while conduction fronts seem to be less important in the ISM.

